
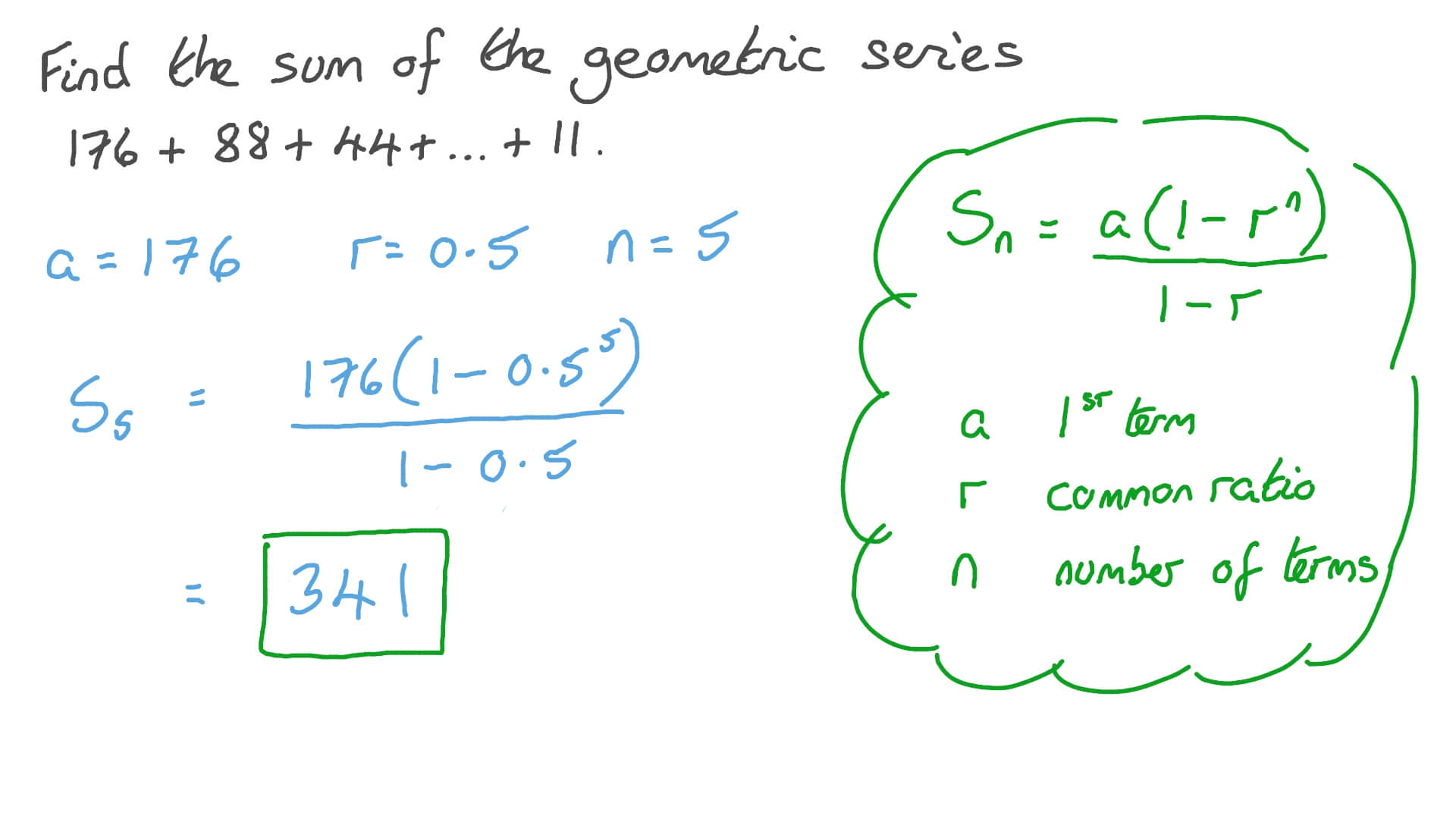
#SOLVING SEQUENCES HOW TO#
Broadly there are three types of sequence or progression 1). In order to work out whether a number appears in a sequence using the n th term we put the number equal to the n th term and solve it. In this explainer, we will learn how to solve real-world applications of arithmetic sequences, where we will find the common difference, th term explicit.
Since there was no difference found between these sequences for either level of element interactivity, the paper discusses conditions of effectiveness of example-based instructions for different knowledge types in the broader context of Explicit Instruction First and Problem-Solving First approaches. Basically there are some rule followed in the sequence and series. An experiment is reported comparing the Problem-Example and Example-Problem sequences on two levels of element interactivity, low versus high, which were associated with two types of conceptual knowledge (general principle knowledge and knowledge of principles underlying procedures, accordingly). This paper takes a deeper look at the effect of types of knowledge concentrating on conceptual knowledge. Khan Academy is a 501(c)(3) nonprofit organization. Our mission is to provide a free, world-class education to anyone, anywhere. For more information about the Encyclopedia, see the Welcome page. The comparative effectiveness of these sequences, however, is subject to the influence of the factors of element interactivity and prior knowledge, and studies have examined these influences focused mostly on procedural rather than conceptual knowledge. We'll construct arithmetic and geometric sequences to describe patterns and use those sequences to solve problems. The On-Line Encyclopedia of Integer Sequences (OEIS) Enter a sequence, word, or sequence number: Hints Welcome Video.

In cognitive load theory, the superiority of the Example-Problem sequence over the Problem-Example sequence has become a classic paradigm.


 0 kommentar(er)
0 kommentar(er)
